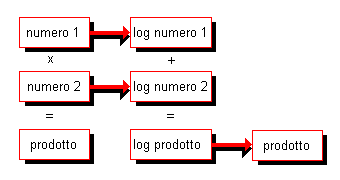
L'operatore logaritmo permette di trasformare prodotti in somme, e anche divisioni in sottrazioni. Ad esempio, nel caso del prodotto di due numeri, si opera come nello schema seguente:
Il procedimento sembra macchinoso, però i logaritmi permettono di fare operazioni anche più complicate di moltiplicazioni e divisioni. Presto vedremo i vantaggi dell'introduzione del logaritmo.
Il significato di questa definizione è sconcertante... ricorda l'inizio di una terzina di Dante: "queste parole di colore oscuro..." , però lo schema seguente aiuta a chiarire la definizione!
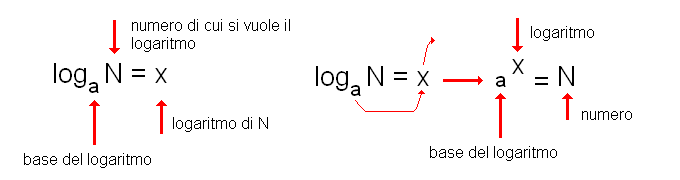
Osservate le frecce nella figura di mezzo: la base, a, si abbassa e colpisce dal basso il logaritmo, X, che salta in alto formando l'eguaglianza della figura a destra. Come si vede, il logaritmo, X, è l'esponente che si deve dare alla base, a, per avere il numero, N, di cui si vuole il logaritmo.
Facciamo un esempio: sia da calcolare log10100 = x
la base 10 dà una spinta al logaritmo, x, che salta in alto portando all'eguaglianza: 10x = 100
dunque, l'eguaglianza è soddisfatta per x = 2. Così, diremo che il logaritmo di 100 in base 10 è 2.
sia da calcolare log101000 = x
questo corrisponde all'eguaglianza: 10x = 1000 che è soddisfatta per x = 3. Così, diremo che il logaritmo di 1000 in base 10 è 3.
sia da calcolare loga a = x
questo corrisponde all'eguaglianza: ax = a che è soddisfatta per x = 1. Così diremo che il logaritmo di un numero, a, calcolato in base, a, è sempre 1. Si faccia attenzione: il logaritmo di 8 in base 8 è 1; il logaritmo di 22 in base 22 è 1; e così via.
abbiamo premesso che il prodotto di due numeri corrisponde alla somma dei logaritmi dei due numeri. Diamone un esempio:
sia da calcolare 1000 · 100 = 100000
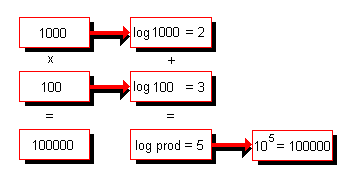
log101000 · 100 = log101000 + log10100 = 3 + 2 = 5
da cui 105 = 100000
In base alla definizione di logaritmo, risulta: log 1 = 0; log 10 = 1; log 100 = 2; log 1000 = 3
log10 0 = x → 0 = 10x = 1/10-x quindi x → - ∞ (perché attribuendo valori sempre più grandi a x, il suo reciproco tende a zero).
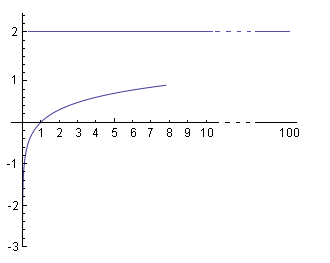
Con questi elementi si può tracciare il grafico della funzione logaritmica (fig. a destra).
Come si vede dal grafico, non esistono (nel campo reale) i logaritmi di numeri negativi; la curva logaritmica tende a - ∞ per x → 0 e interseca l'asse delle x nel punto x = 1 dove assume il valore zero. Inoltre, avvicinandosi all'ordinata y = 1, la pendenza della curva diminuisce lentamente raggiunge y = 2, per x = 100.
I logaritmi permettono alcune importanti applicazioni, e ciò può essere immediatamente compreso con un esempio. Supponiamo di voler collocare su un foglio di carta quadrettata le distanze in una certa scala dei vari pianeti dal Sole. Queste distanze, con buona approssimazione, seguono una progressione geometrica riassunta dalla legge di Titius-Bode. Se sulla carta quadrettata poniamo uguale a un quadretto la distanza Sole-Mercurio, che è di circa 0,4 unità astronomiche (un'unità astronomica. ua, è la distanza tra Terra e Sole), la Terra, verrebbe posta a 2 quadretti e mezzo di distanza, mentre Marte si troverebbe a 4 quadretti. Nettuno, però, mantenendo la stessa scala (1 quadretto = 0.4 ua), andrebbe collocato a 75 quadretti, ossia fuori dal foglio! Fortunatamente Plutone, come pianeta, non fa' più parte del sistema solare.
Se dunque vogliamo disegnare su un normale foglio di carta tutti i pianeti del sistema soalre, dobbiamo ricorrere ad una scala variabile: la scala logaritmica. È sufficiente che ciascun pianeta venga sistemato non alla distanza effettiva dettata dalla scala scelta, bensì al logaritmo di tale distanza (v. fig. a sinistra). In questo modo anche se, per maggior comodità di lettura, fissassimo la distanza Sole-Mercurio in 10 quadretti anziché in uno solo, quella media di Plutone, circa 100 volte superiore, si ridurrebbe a circa una ventina di quadretti restando contenuta all'interno del foglio. E' ovvio che una rappresentazione del genere non rispecchia la realtà, ma fornisce un notevole aiuto visivo e comunque è sempre possibile tornare ad una scala costante con l'operazione inversa, purché... si disponga di un foglio sufficientemente grande.
proprietà 1: log10 N1 · N2 = log10 N1 + log10 N2
il logaritmo di un prodotto è la somma dei logaritmi;
proprietà 2: log10 N1 / N2 = log10 N1 - log10 N2
il logaritmo di un quoziente è la differenza dei logaritmi;
proprietà 3: log10 N1n = n log10 N1
il logaritmo di un numero elevato ad esponente, n, è dato da n volte il logaritmo del numero.
I logaritmi in base 10, brevemente indicati con "log" (quelli in base e sono indicati con "ln"), godono di una particolare proprietà, che introdurremo con un esempio:
con una calcolatrice si compila la tabella seguente:
 |
log 3,5 | 0,544068 |
| log 35 | 1,544068 | |
| log 350 | 2,544068 | |
| log 3500 | 3,544068 | |
| log 0,35 | -0,455931 | |
| log 0,035 | -1,455931 |
Si consideri il numero N · 10n il logaritmo è : log N · 10n = log N + log 10n = log N + n;
per la divisione si ha: N : 10nn = log N - log 10n = log N - n
La regola funziona anche per i numeri negativi: per esempio, log 0,35 = -0,455931 ; questo numero non cambia se vi addizioniamo e contemporaneamente sottraiamo 1: -1 + 1 - 0,455931 = - 1 + 0,544069 = (-)0,455931 ;
analogamente: log 0,035 = -1,455931 e quindi = -1 + 1 - 1,455931 = -1 -0,455931 = (-)1,455931
La regola per i numeri minori di 1 vuole che la mantissa sia preceduta da un numero negativo pari al numero di zeri che seguono la virgola.
sia log10 N1 = x ; loge N1 = y
ovviamente essendo le basi diverse, lo saranno anche i logaritmi, per cui : N1 = 10x ; N1 = ey
essendo uguali i termini a primo membro, N1, devono esserlo anche i termini a secondo membro:
10x = ey
ora applichiamo il logaritmo decimale (in base 10) ad ambo i membri:
log10 10x = log10 ey
per la proprietà 3 dei logaritmi, si ha:
x log10 10 = y log10 e
il log1010 = 1 in quanto è il logaritmo di un mumero calcolato nella stessa base, quindi:
x = y log10 e
ora, considerando che log10 N1 = x ; loge N1 = y
si ottiene la formula di cambiamento di base:
log10 N1 = loge N1 · log10 e
esempio 1: calcolare ln 37 sapendo che il logaritmo in base 10 di 37 è (con la calcolatrice) = 1.5682
log10 N1 = loge N1 · log10 e → 1.568 = loge 37 · log10e
il log10e = 0.4342 (alla quarta decimale) quindi loge 37 = 1.5682/0.4342 = 3.6116 prossimo a quello che si ottiene con la calcolatrice. Digitando il numero 37 e premendo il tasto "ln" (log è per la base 10), si ottiene 3.6109 risultato accettabile per le approssimazioni alla 4 cifra decimale.
esempio 2: calcolare log 37 sapendo che il logaritmo in base e di 37 è (con la calcolatrice) = 3.6109
log10 N1 = loge N1 · log10 e → log10 N1 = 3.6109 · log e
il log e = 0.4342 (alla quarta decimale) quindi log 37 = 3.6109 · 0.4342 = 1.5678 prossimo a quello che si ottiene con la calcolatrice. Digitando il numero 37 e premendo il tasto log (ln è per la base 2), si ottiene 1.5682 risultato accettabile per le approssimazioni alla 4 cifra decimale.
| log 1,1 | 0,04139 | log 6 | 0,77815 |
| log 1,2 | 0,07918 | log 6,1 | 0,78532 |
| ...... | ......... | ||
| log 2 | 0,30102 | log 7 | 0,84509 |
| log 2,1 | 0,32221 | log 7,1 | 0,85125 |
| ..... | |||
| log 3 | 0,47712 | log 8 | 0,90308 |
| log 3,1 | 0,49136 | log 8,1 | 0,90848 |
| ......... | |||
| log 4 | 0,60205 | log 9 | 0,95424 |
| log 4,1 | 0,61278 | log 9,1 | |
| ........ | |||
| log 5 | 0,69897 | ||
| log 5,1 | 0,70757 |
Con lo sviluppo in serie di Mac Laurin (senza ricorrere alla calcolatrice) si possono calcolare i logaritmi naturali dei numeri da 1 a 9.9 con passo 0,1 (1.1 ; 1.2 ; 1.3 ; ...) e da questi con il cambio di base si possono ottenere i logaritmi in base 10.
La tabella a destra riporta i logaritmi decimali dei numeri compresi tra 1 e 9.9 approssimati alla quinta cifra decimale. La stessa tabella, sfruttando le proprietà dei logaritmi, permette di calcolare qualsiasi altro logaritmo (sebbene con approssimazione).
Per esempio, il logaritmo di 21 è uguale a log 2.1 · 10 = log 2.1 + log 10 = 1,32221
il logaritmo di 0,21 è uguale a log 21/10 = log 21 - log 10 = -0,67778
Ovviamente restano da calcolare i logaritmi intermedi, come per esempio 2.5 che possono essere calcolati con una base diversa. Per esempio log5 25 = x da cui si trova x = 2
Con un cambiamento di base [log 25 = log5 25 · log 5] si trova subito il valore cercato:
log 25 = 2 · 0,69897 = 1,39794. Poi, è facile calcolare il log 2.5.
In realtà, le tavole logaritmiche sono molto più complesse di quanto qui esposto unicamente a fini didattici, e d'altra parte sono state rese obsolete dalle calcolatrici tascabili!
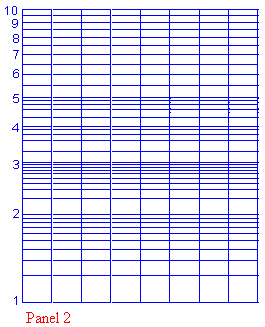
Spesso è laborioso raccogliere un insieme di logaritmi per una relazione del tipo N/N0 riportata nella tavola 3, così si fa uso di una speciale carta per grafici appositamente costruita in modo da farlo direttamente. Un foglio di questa carta è mostrato nella tavola 2. Osservate che essa ha una scala orizzontale lineare, ma la verticale è una scala logaritmica. Questa carta è detta semilogaritmica ad un ciclo. Il significato del nome sarà chiarito fra poco.
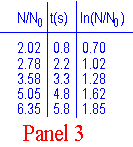
Nella tavola 3, c'è una tavola di valori per N/N0 che segue una relazione esponenziale. Nella parte destra delle colonne è riportato il logaritmo naturale di N/N0.
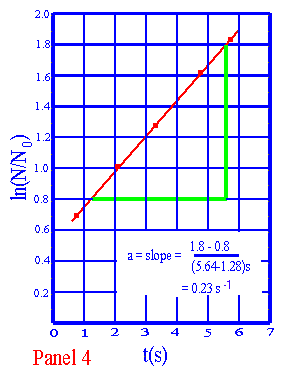Il grafico mostrato nella tavola 4 è una curva dei valori riportati nella tavola 3 contro il tempo t.
Si noti che questo grafico è su una normale carta millimetrata per grafici, non carta semilogaritmica. Useremo la carta semilogaritmica più avanti. Come si può vedere, il grafico è una linea retta su cui possono essere individuate la pendenza e la costante a. Fermiamoci un attimo e controlliamo (riquadro in tavola 4) il calcolo di a.
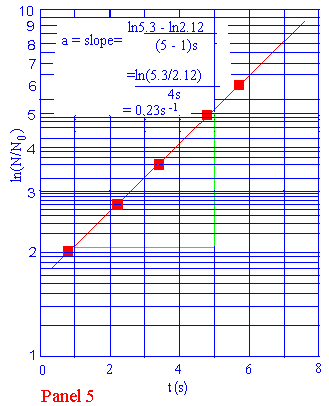Ora vedremo come la carta semilogaritmica utilizzata nella tavola 5 semplifica il calcolo. Qui sono usati gli stessi dati della tavola 3 e, poiché i dati N/N0 sono tutti compresi fra 1 e 10, potremo direttamente usare i numeri sulla parte sinistra della carta semilogaritmica.
Tutto quello che dobbiamo fare è osservare come è suddivisa la carta. In questo esempio, c'è una subdivisione in 0.1 (parti non costanti) da 1 a 3, ma la subdivisione è 0.2 da 3 a 5 e diventa 0.5 da 5 a 10. Soffermiamoci a vedere come è tracciato questo grafico.
Ora proviamo a trovare a. Nuovamente dobbiamo trovare la pendenza e questo richiederà di trovare i logaritmi, ma useremo solo due punti su qualsiasi triangolo per determinare la pendenza. Fermiamoci ancora e controlliamo il calcolo della pendenza sulla tavola 5
Notiamo che dobbiamo considerare solo un logaritmo nel calcolo della pendenza in quanto la differenza di due logaritmi è il logaritmo del quoziente. Naturalmente otterremo lo stesso valore di prima, a = 0.23 s-1 ma con maggior facilità.
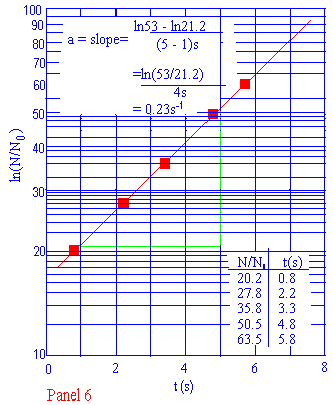Supponiamo, inoltre, che i nostri dati siano quelli mostrati nella tavola compresa nella tavola 6. Ora i valori di t sono gli stessi, ma i valori di N/N0 sono 10 volte maggiori. Cosa dobbiamo fare? La risposta è che la decade posta lungo l'asse verticale è abbastanza arbitraria: può essere da 1 a 10 come in precedenza, o da 10 a 100 come quella proposta, oppure da 100 a 1000, ma anche da 0.1 a 1 e così via. Fermiamoci per capire come è tracciato il grafico nella tavola 6.
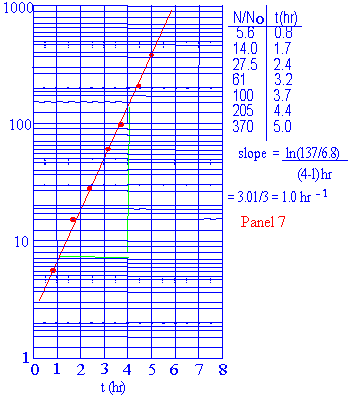Ora supponiamo che abbiate i dati riportati nella tavola della tavola 7. Nessuna delle carte semilogaritmiche che avete visto finora funzionerà. Potreste tracciare il primo numero, o dal secondo al quinto, o dal 5 al 7, o da 10 a 100 o da 100 a 1000, in altre parole una decade. Però ora N/N0 copre parti di 3 decadi, cioè da 1 a 1000. Per questo occorre la carta logaritmica in tre cicli che è stata utilizzata per tracciare questi dati. Fermiamoci e controlliamo il tracciato ed i calcoli sulla tavola 7.
Come potete vedere da questo esempio, si sceglie il numero di cicli per la carta da usare in modo da coprire i dati che si hanno a disposizione: la carta semilogaritmica è a uno, due, tre, ... n cicli.
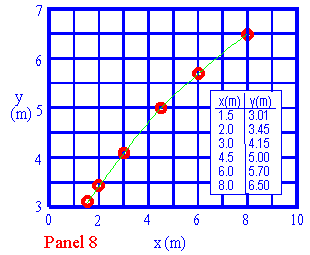
Ora consideriamo un nuovo problema. Supponiamo che abbiate l'insieme di dati riportati nella tavola 8. Nella stessa tavola è anche mostrato un grafico di y contro x, e possiamo vedere che è una curva sottile, Ma oltre questo, essa non è molto informativa. Supponiamo d'altra parte, in aggiunta, che ci siano basi teoriche per credere che questi dati siano ottenuti da una legge di tipo y = axb. Come potremmo verificare se questo è vero e valutare le costanti a e b?
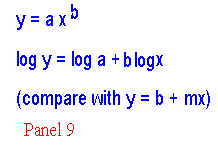Prendiamo il logaritmo di entrambi i membri dell'equazione presente nella tavola 9. Si può vedere che, se y = a xb, allora un grafico di log y contro log x produce una linea retta di pendenza b ed intercetta su y pari a log a. Per conseguenza, se un grafico di log y contro log x per un gruppo di dati è una linea retta, allora i dati seguono la relazione y = a xb. Noi ora potremo guardare a una tavola di valori di log x e log y e tracciarla, ma c'è un modo più semplice per procedere.
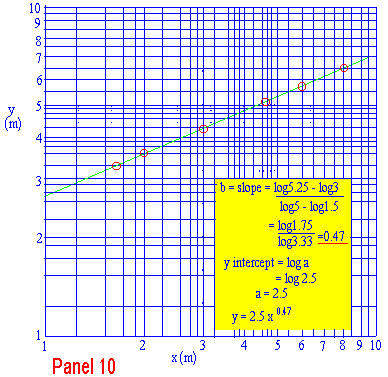Poiché dobbiamo tracciare log y contro log x, dovremo usare carta divisa logaritmicamente su entrambi gli assi. Questa carta è chiamata "carta log-log" oppure "carta logaritmica", ed un esempio ad un ciclo è mostrato nella tavola 10 dove sono riportati i dati della tavola 8. Fermiamoci e cerchiamo di comprendere come sono riportati i punti.
Il grafico è una linea retta così che i dati seguono la legge y = a xb. La costante b è data dalla pendenza. Esaminiamo la tavola 10 e cerchiamo di capire quale valore otterremo. Per calcolare la pendenza, possiamo usare sia logaritmi in base 10 che in base e, a seconda delle necessità. Osservando che i singoli logaritmi non hanno unità, segue che la pendenza non ha unità.
Il valore di log a è lo stesso del valore dell'intercetta y. Per ottenerlo, osserviamo sul grafico il punto dove la variabile orizzontale è 0. Ricordiamo che, essendo l'asse orizzontale logaritmico. la variabile orizzontaòe è log x e non direttamente x, così, se vogliamo il punto dove log x = 0, x deve essere 1. L'intercetta può essere letta fuori dal grafico lungo la linea verticale dove x = 1.
In questo caso, l'intercetta y è log 2.5.Se i valori di x ed y eccedono una decade, allora deve essere utilizzata una carta a più cicli. La carta logaritmica è disponibile in molte combinazioni, come 2x1, 2x3 e 5x3.
1tradotto da: www.physics.uoguelph.ca/tutorials/tutorials.html
 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| HOME PAGE |
|||||||
Marcello Guidotti - copyright 2011